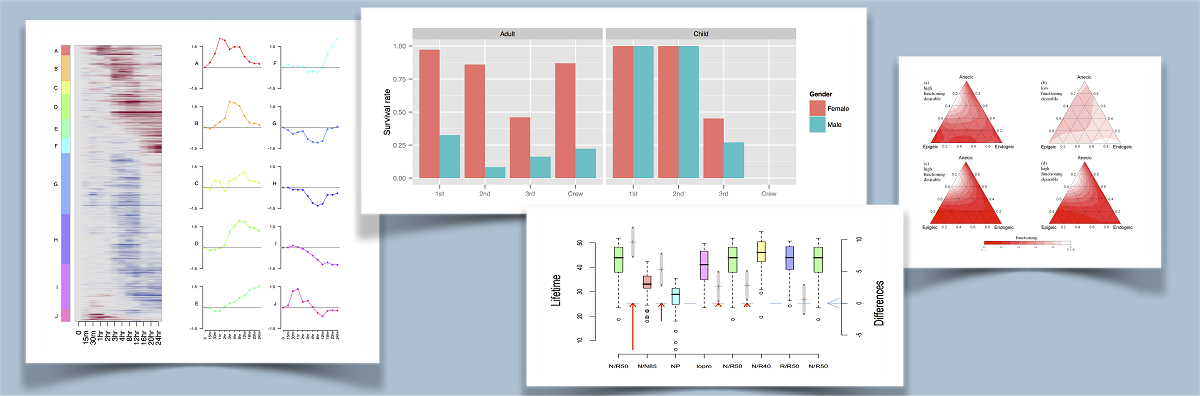
The Department offers a variety of undergraduate and postgraduate degrees in Mathematics and Statistics designed to prepare students for jobs in many different fields. It has research groups in Algebra & Number Theory, Geometric Analysis, Mathematics Education, and Statistics.
Cuireann an Roinn cúrsaí éagsúla fochéime agus iarchéime ar fáil sa Mhatamaitic agus i Staitistic chun mic léinn a ullmhú do phoist i réimsí éagsúla. Tá grúpaí taighde ag an Roinn in Ailgéabar & Uimhirtheoiric, Anailís Gheoiméadrach, Oideachas Matamaitice, agus Staitistic mar aon le clár leathan taighde as a leanann céimeanna M.Sc agus Ph.D., i mórchuid réimsí spreagúla.